이전 글 에서 에라토스테네스의 체를 알아보았습니다.
같은 방법으로 백준 6588, 골드바흐의 추측문제를 풀어보도록 하겠습니당.

먼저 문제를 살펴보면
"4보다 큰 모든 짝수는 두 홀수 소수의 합으로 나타낼 수 있다" 고 합니다.
이 골드바흐의 말을 검증하는 프로그램을 작성하는건데요,
문제의 예시를 표로 정리해 보겠습니다.
| 4 보다 큰 짝수 | 두 홀수 소수 |
| 20 | 3 + 17 |
| 7 + 13 | |
| 42 | 5 + 37 |
| 11 + 31 | |
| 13 + 29 | |
| 19 + 23 |

다음으로 입력을 살펴 보겠습니다.
입력으로는 6 이상, 1,000,000 이하 짝수 정수가 주어진다 합니다.
구해야 할 소수의 범위는 1,000,000 까지임을 알 수 있습니다.
테스트 케이스의 숫자 갯수는 주어지지 않았고, 입력에 0 이 주어지면 테스트 케이스 입력이 더 이상 없다는 뜻이라 합니다.

출력은 n = a + b 형태로 출력합니다.
4 보다 큰 짝수 n을 두 홀수 소수 a , b로 만들 수 있는 방법이 여러개라면
b - a 가 가장 큰 것을 출력하라고 합니다. (아래 그림 참고)

또한 소수 만으로 만들 수 없을 때 "Goldbach's conjecture is wrong." 을 출력하도록 해야합니다.

주어진 조건을 정리해보면 아래와 같습니다.
1. 4 보다 큰 짝수 숫자 입력 받기 (입력에 0 이 주어지면 테스트 케이스 입력이 더 이상 없다.)
2. 소수를 구해야 함. (구해야 할 소수의 범위는 1,000,000 까지임)
3. a + b = n 인지 확인하고 n = a + b 형태로 출력 ( a 와 b 는 소수 , 방법이 여러개라면 b - a 가 가장 큰 것을 출력)
4. 소수 만으로 만들 수 없을 때 "Goldbach's conjecture is wrong." 을 출력
1. 4 보다 큰 짝수 숫자 입력 받기

BufferedReader : new Scanner 보다 빠른 입력을 받을 수 있어 시간 초과를 고려해 사용했습니다.
while (true) : 0 이 나오기 전 까지 계속해 입력받아야 하기 때문에 while(true) 를 사용했습니다.
2. 소수 구하기

boolean 배열 : 이전 글 과 같이 소수를 구하기 위한 배열입니다.
범위는 입력으로 1,000,000 이하 짝수 정수가 주어지기 때문이며, +1은 1,000,000 를 포함하기 위함입니다.
3. a + b = n 인지 확인하고 n = a + b 형태로 출력하기
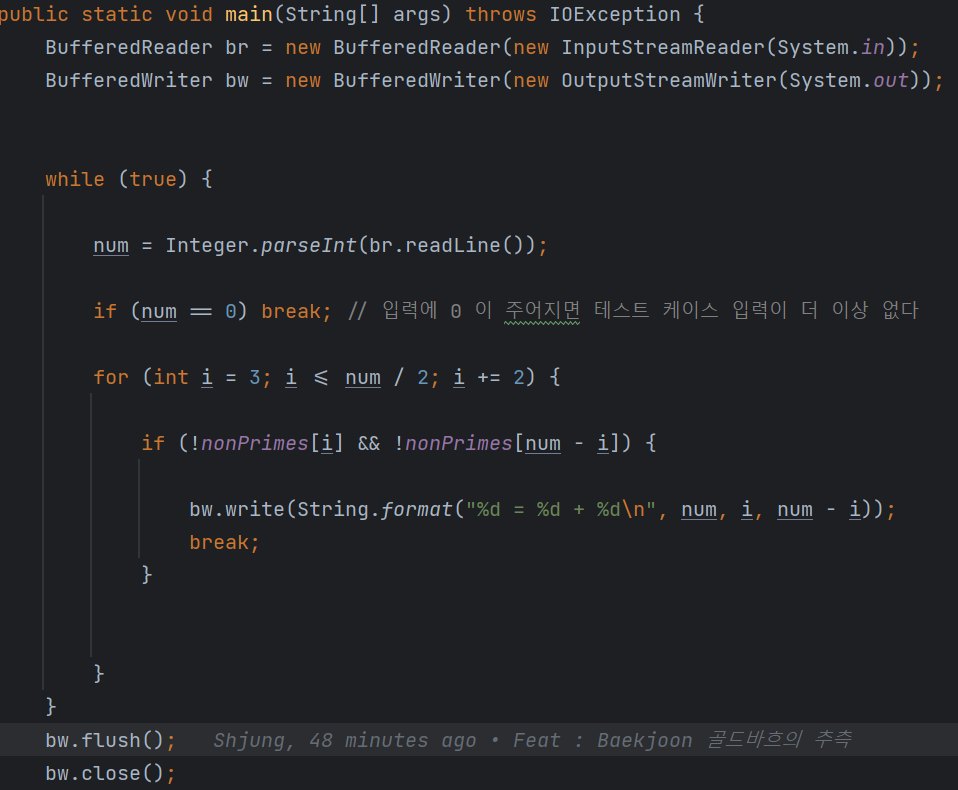
BufferedWriter : System.out.println 보다 조금 더 빠른 출력이 가능하기에 사용했습니다.
BufferedWriter 를 사용했기에 write 와 flush , close 까지 사용해 줍니다.
int i = 3 : 소수 3 부터 n = a + b 가 성립 되는지 확인합니다.
num / 2 : 입력받은 수의 절반을 넘은 수는 검증할 필요가 없습니다.
하나의 소수는 i이고 다른 하나는 (num - i)이므로 i는 num / 2 을 하지 않으면 중복되는 결과가 나오게 됩니다.
반복문 범위를 줄일 수 있습니다.
i += 2 : 시작 수 인 3은 홀 수 이기 때문에 +2 를 계속 한다면 반복문 종료 시 까지 홀수만 검증 합니다. 반복문 범위를 줄일 수 있습니다.
if(!nonPrimes[i] && !nonPrimes[num - i]) : i가 소수이면서 num - i 또한 소수인 수가 있는지 확인합니다.
있다면 n = a + b 형태로 BufferedWriter 에 저장합니다.
b - a 가 가장 큰 것을 출력하기 위해 찾고 난 후 break 로 반복문을 벗어납니다.
4. 소수 만으로 만들 수 없을 때 "Goldbach's conjecture is wrong." 을 출력

i > num / 2 : 3번에서 말했듯 num / 2 보다 큰 숫자가 된 이후에는 중복된 검증입니다.
앞 if 문에서 break 로 반복문을 빠져나가지 못했다면 n = a + b 가 검증 되지 않았다 볼 수 있습니다.
"Goldbach's conjecture is wrong." 해당 문구를 출력하기 위해 작성해 줬습니다.
여기까지 코드
import java.io.*;
public class Main {
static boolean[] nonPrimes = new boolean[1000001];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int num = 0;
for (int i = 2; i * i < nonPrimes.length; i++) {
if (!nonPrimes[i]) {
for (int j = i * i; j < nonPrimes.length; j += i) {
nonPrimes[j] = true;
}
}
}
while (true) {
num = Integer.parseInt(br.readLine());
if (num == 0) break;
for (int i = 3; i <= num / 2; i += 2) {
if(!nonPrimes[i] && !nonPrimes[num - i]){
bw.write(String.format("%d = %d + %d\n",num,i,num - i));
break;
}
else if(i > num / 2){
bw.write("Goldbach's conjecture is wrong.\n");
break;
}
}
}
bw.flush();
bw.close();
}
}
하지만 제출 하니 시간초과입니다.

논리는 맞지만 , 시간초과인것 같아 해결하기 위해 개선할 부분을 찾아보았습니다.
질문 게시판 내용을 토대로 출력 코드를 수정해 보았습니다.
bw.write(String.format("%d = %d + %d\n",num,i,num - i)); → bw.write(num + " = " + i + " + " + (num - i) + "\n");
import java.io.*;
public class Main {
static boolean[] nonPrimes = new boolean[1000001];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int num = 0;
for (int i = 2; i * i < nonPrimes.length; i++) {
if (!nonPrimes[i]) {
for (int j = i * i; j < nonPrimes.length; j += i) {
nonPrimes[j] = true;
}
}
}
while (true) {
num = Integer.parseInt(br.readLine());
if (num == 0) break; // 입력에 0 이 주어지면 테스트 케이스 입력이 더 이상 없다
for (int i = 3; i <= num / 2; i += 2) {
if (!nonPrimes[i] && !nonPrimes[num - i]) {
bw.write(num + " = " + i + " + " + (num - i) + "\n"); // 수정된 부분
break;
}
else if (i > num / 2) {
bw.write("Goldbach's conjecture is wrong.\n");
break;
}
}
}
bw.flush();
bw.close();
}
}
그랬더니 !

ㅎㅎㅎㅎ 이상입니다.
'Algorithm' 카테고리의 다른 글
| [ Algorithm ] 에라토스테네스의 체 ( feat . 백준 1929 - 소수 구하기 ) (0) | 2023.09.24 |
|---|---|
| [Algorithm] 시간 복잡도와 빅 오 (Big-O Notation) (0) | 2023.06.01 |