[ Algorithm ] 에라토스테네스의 체 ( feat . 백준 1929 - 소수 구하기 )

 

수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.

 

위키백과

소수 구하는 문제는 에라토스테네스의 체를 이용하는게 가장 편리합니다.

소수란 ?  양의 약수를 두 개만 가지는 자연수. 1과 자기자신으로만 나누어지는 수

 

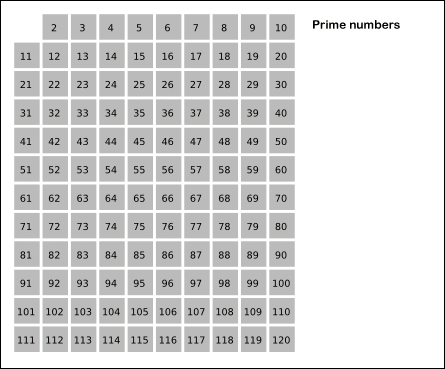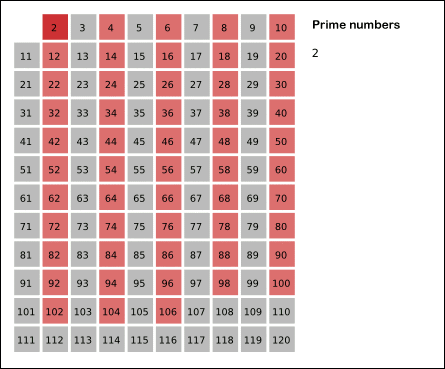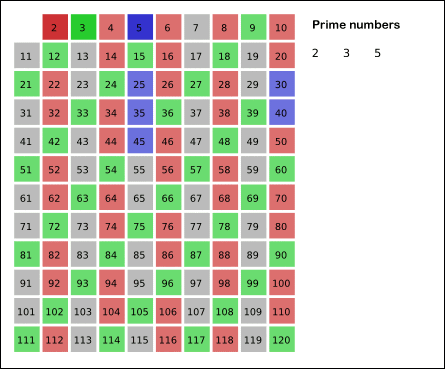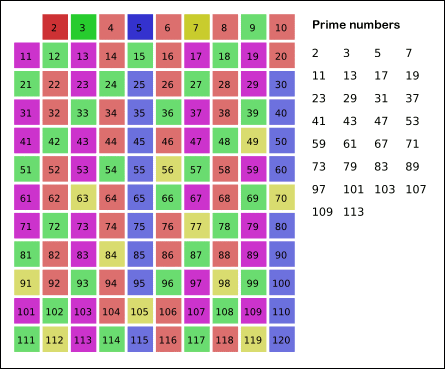
위키 백과에서 가져온 그림을 토대로 설명을 하면,

 

2 부터 목표 수(120) 사이 자기 자신을 제외 한 자신 배수를 모두 지우는 것입니다.

 

자바 코드로 살펴보겠습니다.

public class Eratos {

    public static void main(String[] args){

        int start = 1;
        int end = 120;
		
        // 소수인지 판별하기 위해 길이가 end + 1 인 배열 선언
        // 마지막 수도 포함 하기 위해 (end + 1)사용 함.
        // nonPrimes 이 false 라면 소수.
        boolean[] nonPrimes = new boolean[end + 1];

        nonPrimes[0] = nonPrimes[1] = true; // 0 과 1 은 소수가 아님.

		// 에라토스테네스의 체 알고리즘
        for (int i = 2; i * i <= end; i++) { // 2 부터 시작해 i * i 가 end를 넘지 않을 때 까지 반복.
            if (!nonPrimes[i]){ // nonPrimes 이 false 라면
                for (int j = i * i; j <= end; j += i) { // j 는 i * i 부터 시작, 한 번 반복 시 j + i 를 함.
                    nonPrimes[j] = true; // i * i 와 j + i 는 i 의 배수가 됨 => 소수가 아님
                }
            }
        }
		
        // 소수 출력
        for (int i = start; i <= end ; i++) {
            if(!nonPrimes[i]){ 
                System.out.println(i);
            }
        }
    }
}

++ 반복문의 범위 i * i 

소수 구할 때 효율성을 높이기 위함. 

 

반복문 조건	시간 복잡도
i <= end	O(n)
i * i <= end 또는 i <= Math.sqrt(end)	O(n log log n)

i 가 제곱되어 end 보다 커지면 반복문이 종료.

i 제곱으로 평가되지 못한 수는 i 보다 작은 수가 이미 처리함. (위키피디아 그림 참고.)

 

 

백준 1929 , 소수 구하기에 적용해 보겠습니다.

 

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] numList = br.readLine().split(" ");

        int start = Integer.parseInt(numList[0]);
        int end = Integer.parseInt(numList[1]);

        boolean[] nonPrimes = new boolean[end + 1];

        isPrime[0] = nonPrimes[1] = true;

        for (int i = 2; i * i <= end; i++) {
            if (!nonPrimes[i])
                for (int j = i * i; j <= end; j += i) {
                    nonPrimes[j] = true;
                }
        }

        for (int i = start; i <= end ; i++) {
            if(!nonPrimes[i]){
                System.out.println(i);
            }
        }
    }

}